Medzi tieto sa asi najskor pocitaju uz spomenute
XOR
Dekoder
Enkoder
Multiplexor
Demultiplexor
Scitacka
Tak hor sa do citania ;)
Tuesday, May 31, 2011
HW: Scitacka
Povedzme si najprv, co na to wikipedia.
"Binárna sčítačka (alebo len sčítačka) je kombinačný logický obvod, realizujúci sčítanie čísel, reprezentovaných v binárnej číselnej sústave. Tvorí dôležitú súčasť aritmeticko-logickej jednotky (ALU) centrálneho procesora (CPU) počítača. V prípade použitia dvojkového doplnkového kódovania záporných čísel sa dá sčítačka veľmi jednoducho rozšíriť na sčítačku-odčítačku."
Takze, navrhujeme kombinacny logicky obvod, ktory dokaze scitat binarne cisla. Zacneme polovicnou scitackou, ktora scitava dva jednobitove scitance a vystupom je sucet a prenos do vyssieho radu. Rozdiel medzi polovicnou a uplnou scitackou je, ze polovicna prenos nedokaze spocitat prenos z predchadzajuceho radu, zatial co uplna dokaze.
Polovicna scitacka (Half Adder)
IN: scitance a, b
OUT: vysledok s a prenos q
Pravdivostna tabulka
a b | q s
--------------------
0 0 | 0 0 a odtialto vysledne rovnice
0 1 | 0 1 s = a XOR b
1 0 | 0 1 q = a.b
1 1 | 1 0
V tejto chvili by sme uz mali byt schopny navrhnut obvod pre polovicnu scitacku (c na obrazku je rovne q v rovnici)
Uplna scitacka
Uplna scitacka dokaze spracovat prenos z nizsieho radu a lahko ju ziskame zlozenim dvoch polovicnych scitaciek.
a b p | s q
----------------------
0 0 0 | 0 0
0 0 1 | 1 0
0 1 0 | 1 0
0 1 1 | 0 1
1 0 0 | 1 0
1 0 1 | 0 1
1 1 0 | 0 1
1 1 1 | 1 1
Rovnice v tomto pripade uz nie su take priamociare a mozme pouzit karnaughove mapy, aby sme ziskali minimalizovane verzie, hoci tolko uz dokazeme aj z tabulky :). Vysledok bude nasledujuci:
s = a'b'p + a'bp' + ab'p' + abp = p(a'b' + ab) + p'(a'b + ab') = p + p'(a XOR b) = p XOR a XOR b
q = a'bp + ab'p + abp' + abp = ab(p + p') + p(a'b + ab') = ab + p(a XOR b)
Tu sa ukazuje, preco su mapy dobry napad ;) Ak pouzijeme mapy, tak vysledok pre q by mal byt ap + bp + ab = ab + p(a XOR b) ??? (tak toto si treba zistit).
Pre nakres obvodu som si pozical pekny obrazok z wiki, kde su farebne oddelene jednotlive pol-scitacky.
A je hotovo ;)
http://www.copsu.cz/mikrop/didakticka_pomucka/cislicova_technika/komb_log_obvody/uplna_scitacka/uplna_scitacka.html
http://www.copsu.cz/mikrop/didakticka_pomucka/cislicova_technika/komb_log_obvody/polov_scitacka/polovicni_scitacka.html
"Binárna sčítačka (alebo len sčítačka) je kombinačný logický obvod, realizujúci sčítanie čísel, reprezentovaných v binárnej číselnej sústave. Tvorí dôležitú súčasť aritmeticko-logickej jednotky (ALU) centrálneho procesora (CPU) počítača. V prípade použitia dvojkového doplnkového kódovania záporných čísel sa dá sčítačka veľmi jednoducho rozšíriť na sčítačku-odčítačku."
zdroj: wikipedia.sk
Polovicna scitacka (Half Adder)
IN: scitance a, b
OUT: vysledok s a prenos q
Pravdivostna tabulka
a b | q s
--------------------
0 0 | 0 0 a odtialto vysledne rovnice
0 1 | 0 1 s = a XOR b
1 0 | 0 1 q = a.b
1 1 | 1 0
V tejto chvili by sme uz mali byt schopny navrhnut obvod pre polovicnu scitacku (c na obrazku je rovne q v rovnici)
Schematicka znacka polovicnej scitacky je dost intuitivna :) a najdete ju v obrazku pre uplnu scitacku, ktora vo svojej znacke nema zlomok 1/2.
Uplna scitacka
Uplna scitacka dokaze spracovat prenos z nizsieho radu a lahko ju ziskame zlozenim dvoch polovicnych scitaciek.
a b p | s q
----------------------
0 0 0 | 0 0
0 0 1 | 1 0
0 1 0 | 1 0
0 1 1 | 0 1
1 0 0 | 1 0
1 0 1 | 0 1
1 1 0 | 0 1
1 1 1 | 1 1
Rovnice v tomto pripade uz nie su take priamociare a mozme pouzit karnaughove mapy, aby sme ziskali minimalizovane verzie, hoci tolko uz dokazeme aj z tabulky :). Vysledok bude nasledujuci:
s = a'b'p + a'bp' + ab'p' + abp = p(a'b' + ab) + p'(a'b + ab') = p + p'(a XOR b) = p XOR a XOR b
q = a'bp + ab'p + abp' + abp = ab(p + p') + p(a'b + ab') = ab + p(a XOR b)
Tu sa ukazuje, preco su mapy dobry napad ;) Ak pouzijeme mapy, tak vysledok pre q by mal byt ap + bp + ab = ab + p(a XOR b) ??? (tak toto si treba zistit).
Pre nakres obvodu som si pozical pekny obrazok z wiki, kde su farebne oddelene jednotlive pol-scitacky.
A je hotovo ;)
http://www.copsu.cz/mikrop/didakticka_pomucka/cislicova_technika/komb_log_obvody/uplna_scitacka/uplna_scitacka.html
http://www.copsu.cz/mikrop/didakticka_pomucka/cislicova_technika/komb_log_obvody/polov_scitacka/polovicni_scitacka.html
HW: XOR
Z predchadzajucich clankov je XOR uz pomerne jednoduchou zalezitostou.
Z pravdivostnej tabulky vieme, ze:
x y F
------------
0 0 0
0 1 1
1 0 1
1 1 0
a teda ab' + a'b
Saturday, May 21, 2011
HW: Demultiplexor
Demultiplexor je "opakom" multiplexoru. Takze tu bude jeden vstup a viac vystupov :).
Porovnanie tejto schemy s multiplexorom nam celkom jasne naznaci, co DEMUX vlastne je. Jeden vstup je "prepnuty" na jeden z vystupov podla hodnoty "selectorov" a,b. Logika je naznacena v pravidvostnej tabulke. Tabulka zobrazuje, ktory vystup sa pouzije. Dolezite je, ze ak vstupom je logicka 1ka, tak vystupom je tiez 1ka, otazka je kde. Pokial by to bola 0, tak vystup je 0 vzdy.
Address OUT
a b
-----------------
0 0 A
0 1 B
1 0 C
1 1 D
F = a'b'A + a'bB + ab'C + abD
DEMUX je opat kombinacny obvod a jeho schema je tu:
Schematicka znacka DEMUXu
Literatura
http://www.electronics-tutorials.ws/combination/comb_3.html
http://lob.felk.cvut.cz/x36lob/downloads/s_typkomb.pdf
Porovnanie tejto schemy s multiplexorom nam celkom jasne naznaci, co DEMUX vlastne je. Jeden vstup je "prepnuty" na jeden z vystupov podla hodnoty "selectorov" a,b. Logika je naznacena v pravidvostnej tabulke. Tabulka zobrazuje, ktory vystup sa pouzije. Dolezite je, ze ak vstupom je logicka 1ka, tak vystupom je tiez 1ka, otazka je kde. Pokial by to bola 0, tak vystup je 0 vzdy.
Address OUT
a b
-----------------
0 0 A
0 1 B
1 0 C
1 1 D
F = a'b'A + a'bB + ab'C + abD
DEMUX je opat kombinacny obvod a jeho schema je tu:
Schematicka znacka DEMUXu
Literatura
http://www.electronics-tutorials.ws/combination/comb_3.html
http://lob.felk.cvut.cz/x36lob/downloads/s_typkomb.pdf
HW: Multiplexor
Opat sa jedna o zariadenie, ktore je tvorene kombinacnym obvodom. Pouzivaju sa v obvodoch, kde jedna datova cesta je vyuzivana viacermi signalmi.
Vyssie znazorneny priklad MUXu ukazuje jeho princip. Iba jeden spinac je zopnuty v tom istom case a ten je vybrany pomocou signalu a,b. Vystup je jeden a je rovny prepojenemu vstupu.
Pravdivostna tabulka MUXu z tohto prikladu musi kombinovat "selectory" A0, A1, ktore urcia vystup, na ktorom je vlastne vstup :) - pretoze z horneho obrazku vidime, ze sa vstup len prepoji na vystup.
Adresa OUT
A0 A1 Y
----------------
0 0 D0
0 1 D1
1 0 D2
1 1 D3
Rovnicu z pravdivostnej tabulky zostavime takto:
Y = a0'a1'D0 + a0'a1D1 + a0a1'D2 + a0a1D3
Realizacia MUXu pomocou kombinacnych prvkov:
Nenechajte sa pomylit, ze multiplexory su limitovane na jeden vystup. Existuju aj multiplexory 4 na 2, 8 na 3, alebo 16 na 4 a pod.
MUXy nachadzaju pouzitie v smerovani signalov, kontrola signalov na datovej zbernici, v optickych kabloch atd. Jeho "opakom" je demultiplexor.
Literatura
http://www.electronics-tutorials.ws/combination/comb_2.html
http://lob.felk.cvut.cz/x36lob/downloads/s_typkomb.pdf
Vyssie znazorneny priklad MUXu ukazuje jeho princip. Iba jeden spinac je zopnuty v tom istom case a ten je vybrany pomocou signalu a,b. Vystup je jeden a je rovny prepojenemu vstupu.
Pravdivostna tabulka MUXu z tohto prikladu musi kombinovat "selectory" A0, A1, ktore urcia vystup, na ktorom je vlastne vstup :) - pretoze z horneho obrazku vidime, ze sa vstup len prepoji na vystup.
Adresa OUT
A0 A1 Y
----------------
0 0 D0
0 1 D1
1 0 D2
1 1 D3
Rovnicu z pravdivostnej tabulky zostavime takto:
Y = a0'a1'D0 + a0'a1D1 + a0a1'D2 + a0a1D3
Realizacia MUXu pomocou kombinacnych prvkov:
Nenechajte sa pomylit, ze multiplexory su limitovane na jeden vystup. Existuju aj multiplexory 4 na 2, 8 na 3, alebo 16 na 4 a pod.
MUXy nachadzaju pouzitie v smerovani signalov, kontrola signalov na datovej zbernici, v optickych kabloch atd. Jeho "opakom" je demultiplexor.
Literatura
http://www.electronics-tutorials.ws/combination/comb_2.html
http://lob.felk.cvut.cz/x36lob/downloads/s_typkomb.pdf
HW: Enkoder
Enkoder je opakom dekoderu. Binarny dekoder premiena vstup na vystup, tak, ze vzdy je aktivna len jedna vystupna premenna. Binarny enkoder zase prijima vzdy jednu aktivnu premennu na vstupe a vystupom je zakodovany stav. V kazdom pripade, ak ste sa v clanku o dekoderi docitali do konca, tak ste si urcite vsimli, ze jeden vystup nie je pravidlom ;).
Pre prioritne enkodery a 8 to 3 enkodery doporucujem precitat http://www.electronics-tutorials.ws/combination/comb_4.html.
Prebrate z http://www.electronics-tutorials.ws
Binarny enkoder je teda logicky kombinacny obvod, ktory premiena logicke hodnoty 1 na vstupe na binarny kod na vystupe.
HW: Dekoder
Dekoder je kombinacny obvod, ktory premiene vstupny binarny kod na vystupny kod. Vstup binarneho dekoderu pozostava z n vstupnych premennych a 2^n vystupnych premenych. Vzdy je aktivny len jeden vystup v zavislosti na vstupe. Vystup dekoderu je (zvycajne) viac bitovy kod ako je kod privedeny na vstup a najpraktickejsie priklady zahrnaju dekodery 2 na 4, 3 na 8 a 4 na 16.
Dekoder 2 na 4 je znazorneny na obrazku.
Pravdivostna tabulka pre dekoder:
IN OUT
x0 x1 | y0 y1 y2 y3
------------------------------------
0 0 | 1 0 0 0
0 1 | 0 1 0 0
1 0 | 0 0 1 0
1 1 | 0 0 0 1
Pri kazdej kombinacii vstupnych premennych je aktivna len jedna vystupna premenna. Podla toho, ktora vystupna premenna nadobuda hodnotu log. 1cky, vieme urcit kombinaciu vstupnych premennych. Tento dekoder te dekoduje vstupny kod.
Ako uz bolo spomenute, dekoder je vlastne kombinacny obvod. Realizacia vyssie spomenuteho binarneho dekoderu vyzera takto:
Dalsim zaujimavym prikladom je dekoder kodu 2z5 (typ 74210 alebo 84210) do kodu BCD (binarne zakodovane desiatkove cislo). Kod 2z5 znamena, ze z 5 moznych bitov budu vzdy 2 jednickove. Taketo cislo budeme volat kodove slovo. Typ 74210 a 84210 urcuje vahu jednotlivych premennych. Vaha urcuje, akou mierou sa premenna prejavi na vystupe, ak nadobuda log. hodnoty 1. Pri 5 bitoch, kde vzdy pouzijeme 2 (bez opakovania :)), mozme zobrazit maximalne 10 cisel.
Dec BCD kod 2z5 kod 2z5
DCBA 74210 84210
0 0000 11000 10100 # v kode 84210 je vysledny sucet vah 10, to je "out of range"
1 0001 00011 00011 a preto ho mozme priradit 0e
2 0010 00101 00101
3 0011 00110 00110
4 0100 01001 01001
5 0101 01010 01010
6 0110 01100 01100
7 0111 10001 11000 # v kode 84210 je vysledny sucet vah 12, to je "out of range",
8 1000 10010 10001 ale nie je iny sposob ako zapisat cislo 7 ...
9 1001 10100 10010
Prevodnik z kodu 2z5 do BCD znamena, ze na vstupe bude 5 premennych a na vystupe 4. Jedna sa o kombinacny obvod, ktory tento kod prevedie. Pre realizaciu pomocou hradiel by sme museli pouzit 5 karnaughovych map a hladat skupinove termy pomocou skupinovej minimalizacie. Ale to je na inokedy :).
Pre zaujimavost: http://www.electronics-tutorials.ws/combination/comb_6.html.
Literatura:
http://dce.felk.cvut.cz/lor/prednasky/skripta/kap2_1.pdf
http://class.pedf.cuni.cz/jancarik/download/kodovanidat.pdf
http://en.wikipedia.org/wiki/Two-out-of-five_code
Dekoder 2 na 4 je znazorneny na obrazku.
IN OUT
x0 x1 | y0 y1 y2 y3
------------------------------------
0 0 | 1 0 0 0
0 1 | 0 1 0 0
1 0 | 0 0 1 0
1 1 | 0 0 0 1
Pri kazdej kombinacii vstupnych premennych je aktivna len jedna vystupna premenna. Podla toho, ktora vystupna premenna nadobuda hodnotu log. 1cky, vieme urcit kombinaciu vstupnych premennych. Tento dekoder te dekoduje vstupny kod.
Ako uz bolo spomenute, dekoder je vlastne kombinacny obvod. Realizacia vyssie spomenuteho binarneho dekoderu vyzera takto:
Prevziate z http://www.electronics-tutorials.ws
Dec BCD kod 2z5 kod 2z5
DCBA 74210 84210
0 0000 11000 10100 # v kode 84210 je vysledny sucet vah 10, to je "out of range"
1 0001 00011 00011 a preto ho mozme priradit 0e
2 0010 00101 00101
3 0011 00110 00110
4 0100 01001 01001
5 0101 01010 01010
6 0110 01100 01100
7 0111 10001 11000 # v kode 84210 je vysledny sucet vah 12, to je "out of range",
8 1000 10010 10001 ale nie je iny sposob ako zapisat cislo 7 ...
9 1001 10100 10010
Prevodnik z kodu 2z5 do BCD znamena, ze na vstupe bude 5 premennych a na vystupe 4. Jedna sa o kombinacny obvod, ktory tento kod prevedie. Pre realizaciu pomocou hradiel by sme museli pouzit 5 karnaughovych map a hladat skupinove termy pomocou skupinovej minimalizacie. Ale to je na inokedy :).
Pre zaujimavost: http://www.electronics-tutorials.ws/combination/comb_6.html.
Literatura:
http://dce.felk.cvut.cz/lor/prednasky/skripta/kap2_1.pdf
http://class.pedf.cuni.cz/jancarik/download/kodovanidat.pdf
http://en.wikipedia.org/wiki/Two-out-of-five_code
Tuesday, May 17, 2011
HW: Rottove mriezky
Pri realizacii logickych funkcii pomocou hradiel NAND a NOR potrebujeme mat fciu v "spravnom tvare", MNKF alebo MNDF. Fcie musime do tohto tvaru casto upravit a namiesto pouzivania boolovej algebry, mozme pouzit techniku nazvanu rottove mriezky. Rottove mriezky su vlastne grafickym znazonrenim De Morganovych zakonov. Zjednodusuju ich aplikaciu a hladanie ekvivalentneho vyjadrenia povodnej funkcie. s pozadovanymi obvodovymi prvkami s lubovolnym poctom vstupov. Teda, boolovej algebry sa nezbavime, ale upravovat budeme graficky, cim eliminujem pocet moznych chyb.
Rott bol inzininier z Prahy 10, ktory tuto metodu analyzy a syntezy kombinacnych obvodov navrhol vo svojej dizertacnej praci zaoberajucej sa dekompoziciou booleovskych vyrazov. Rottove mriezky vychadzaju z de Morganovych zakonov.
Pravidla vytvarania Rottovych mriezok by sa daju zhrnut takto [1]:
Dolezite je, ze rozdelenie do skupin, si mozme urcit viac-menej sami a tak mozme zarucit realizaciu pomocou hradiel so ziadanym poctom vstupov. Zaroven, pri spravnom ukonceni delenia dosiahneme pouzitia iba urciteho typu hradiel. Preto je tato metoda vhodna pre realizaciu pomocou napriklad NAND/NOR s danym poctom vstupov.
Napriklad f(b,a) = a' + b' chceme znazornit pomcou NAND. Pomocou rottovej mriezky zobrazime:
a' + b' -> original
------------ -> znaznornuje 2 vstupove hradlo NAND a celkovu negaciu 2 zapisu rozkladanej log.
| fcie (De Morgan)
a | b -> vstupne premenne odpovedaju vodicom
nas NAND bude mat 2 vstupy, a,b.
Fciu f(x0, x1, x2, x3) = x3 + x0x2 + x0'x1x2 rozlozime pomocou rottovych mriezok pre realizaciu s pouzitim iba NAND a iba NOR prvkov.
NAND:
x3 + x0 . x2 + x0' . x1 . x2
-------------------------------------------------------
| + | + +
| -------------- | --------------------------
| | | | |
x3' . x0 . x2 . x0' . x1 . x2
NOR:
x3 + x0 . x2 + x0' . x1 . x2
----------------------------------------------
. + . + +
----------------------------------------------
| . | . .
| -------------- | ----------------------
| | | |
x3 + x0' + x2' + x0 + x1' + x2'
Funkciu f(d,c,b,a) = a + b'c + cd' budeme realizovat pomocou NAND. Zadana funkcia je v MNDF, ale my potrebujeme MNKF. A tu prichadzaju na rad rottove mriezky.
a + (b' . c) + (c . d')
--------------------------- -> 3 vstupove hradlo NAND
.| + | +
| ---------- | -------- -> 2x 2vstupove hradlo NAND
| | | |
| | | | -> negacia je invertor
a' | b' | c | c | d' -> vstupne premenne, kt. odpovedaju vodicom
a sa zmenilo na a', co vyhovuje de morganovym zakonom. V rottovych mriezkach dochadza k negacii vzdy cez neparnu uroven.
Porovname tento vysledok s vysledkom v kapitole o realizacii log. fcii pomocou hradiel a zistime, ze vysledok je rovnaky. Vyhodou rottovych mriezok teda je ulahcenie prace pri upravach vyrazov.
Ak chceme realizovat zapojenie pomocou hradiel NOR, tak mame dva sposoby, ako na to.
Priklad: f(d,c,b,a) = b(a' + c)(c' + d)
b . ( a' + c ) . ( c' + d )
-------------------------------------
| . | .
| --------------- | ----------------
| | | |
| | | |
b' a' c c' d
Rott bol inzininier z Prahy 10, ktory tuto metodu analyzy a syntezy kombinacnych obvodov navrhol vo svojej dizertacnej praci zaoberajucej sa dekompoziciou booleovskych vyrazov. Rottove mriezky vychadzaju z de Morganovych zakonov.
Pravidla vytvarania Rottovych mriezok by sa daju zhrnut takto [1]:
- celkovu mnozinu vstupnych premennych oznacime vodorovnou ciarou. Jedna sa teda o celkovu negaciu rozkladanej fcie, tak ako urcuje De Morganovo pravidlo
- rozdelime skupiny na podskupiny podla aplikovaneho logickeho prvku
- delime, az kym neeliminujeme vsetky neziaduce logicke operacie
- premenne maju rovnaku alebo negovanu log. hodnotu (podla poctu ciar rozkladu)
- vodorovne ciary predstavuju negaciu nad skupinou vybranych vstupov
- zvisle ciary su umiestnovane podla typu aplikovaneho log. prvku a oddeluju jednotlive skupiny vybranych vstupov log. prvkov.
Dolezite je, ze rozdelenie do skupin, si mozme urcit viac-menej sami a tak mozme zarucit realizaciu pomocou hradiel so ziadanym poctom vstupov. Zaroven, pri spravnom ukonceni delenia dosiahneme pouzitia iba urciteho typu hradiel. Preto je tato metoda vhodna pre realizaciu pomocou napriklad NAND/NOR s danym poctom vstupov.
Napriklad f(b,a) = a' + b' chceme znazornit pomcou NAND. Pomocou rottovej mriezky zobrazime:
a' + b' -> original
------------ -> znaznornuje 2 vstupove hradlo NAND a celkovu negaciu 2 zapisu rozkladanej log.
| fcie (De Morgan)
a | b -> vstupne premenne odpovedaju vodicom
nas NAND bude mat 2 vstupy, a,b.
Fciu f(x0, x1, x2, x3) = x3 + x0x2 + x0'x1x2 rozlozime pomocou rottovych mriezok pre realizaciu s pouzitim iba NAND a iba NOR prvkov.
NAND:
x3 + x0 . x2 + x0' . x1 . x2
-------------------------------------------------------
| + | + +
| -------------- | --------------------------
| | | | |
x3' . x0 . x2 . x0' . x1 . x2
NOR:
x3 + x0 . x2 + x0' . x1 . x2
----------------------------------------------
. + . + +
----------------------------------------------
| . | . .
| -------------- | ----------------------
| | | |
x3 + x0' + x2' + x0 + x1' + x2'
Funkciu f(d,c,b,a) = a + b'c + cd' budeme realizovat pomocou NAND. Zadana funkcia je v MNDF, ale my potrebujeme MNKF. A tu prichadzaju na rad rottove mriezky.
a + (b' . c) + (c . d')
--------------------------- -> 3 vstupove hradlo NAND
.| + | +
| ---------- | -------- -> 2x 2vstupove hradlo NAND
| | | |
| | | | -> negacia je invertor
a' | b' | c | c | d' -> vstupne premenne, kt. odpovedaju vodicom
a sa zmenilo na a', co vyhovuje de morganovym zakonom. V rottovych mriezkach dochadza k negacii vzdy cez neparnu uroven.
Porovname tento vysledok s vysledkom v kapitole o realizacii log. fcii pomocou hradiel a zistime, ze vysledok je rovnaky. Vyhodou rottovych mriezok teda je ulahcenie prace pri upravach vyrazov.
- navrhneme zapojenie pomocou NANDov
- nahradime hradla NAND hradlami NOR
- znegujeme vstupne premenne
- znegujeme vystupne premenne
Priklad: f(d,c,b,a) = b(a' + c)(c' + d)
b . ( a' + c ) . ( c' + d )
-------------------------------------
| . | .
| --------------- | ----------------
| | | |
| | | |
b' a' c c' d
Literatura:
Saturday, May 14, 2011
HW 1.3 Realizace pomocí hradel
V tejto kapitole si povieme, ako realizovat zariadenie, ktore sa chova podla zadanej logickej funkcie. K tomu budeme potrebovat nejake suciastky, a sice hradla, univ. moduly a pamate.
Aby to bolo jednoduchsie :), tak hradla mozme zakreslit aj inym sposobom. Priklad:
Hradla NAND a NOR tvoria uplny subor logickych funkcii. Z toho vyplyva, ze vystacime s jednym typom hradla pre realizaciu vsetkych funkcii.
Realizacia pomocou hradiel NAND
f(d,c,b,a) = a + b'c + cd'
Funckia je zadana v MNDF, ale pre realizaciu s NAND potrebujeme MNKF.
To dokazeme pomocou dvojitej negacie.
f = a + b'c + cd'
f'' = ((a'.(b'c)').(cd')')'
Ako sme na to prisli? Podla pravidla, ze pre realizaciu logickych operacii + a . pouzivame hradlo NAND a to tak, ze premenne vstupujuce priamo do hradla na neparnej urovni od konca musia byt negovane. Hmm ... zacnime od zaciatku. Na uplnom zaciatku mame 4 hradla, do ktorych "vedie" jedna premenna. Podla pravdivostnej tabulky hradla NAND posobi hradlo v tomto pripade ako invertor 1 NAND 1 = 0, 0 NAND 0 = 1. To znamena, ze sme premennu a,b a d znegovali. Term b'c a cd' je snad uz teraz uplne jednoznacny. Teraz ste si urcite vsimli, ze a vstupuje do hradla presne naopak, ako by sme ho cakali :) - a to je presne podla pravidla. Totiz, tesne pred poslednym hradlom mame situaciu: a', (b'c)', (cd')'.
0. uroven: a, b, c, d
1. uroven: a', b', c, d'
2. uroven: a', (b'c)', (cd')'
3. uroven: vstup do hradla: a', (b'c)', (cd')'
Realizacia pomocou hradiel NOR
f(d,c,b,a) = b(a' + c)(c' + d)
f''(d,c,b,a) = (b' + (a' + c)' + (c' + d)')'
Pravidlo pre realizciu pomocou NOR znie: pre realizaciu logickych operacii + a . pouzivame hradlo NOR a to tak, ze premenne vstupujuce priamo do hradla na neparnej urovni od konca musia byt negovane.
A namiesto pocitania pomocou De Morganovych zakonov sme v oboch pripadoch mohli pouzit Rottove mriezky.
Literatura
http://www.electronics-tutorials.ws/combination/comb_1.html
Hradla NAND a NOR tvoria uplny subor logickych funkcii. Z toho vyplyva, ze vystacime s jednym typom hradla pre realizaciu vsetkych funkcii.
Realizacia pomocou hradiel NAND
f(d,c,b,a) = a + b'c + cd'
Funckia je zadana v MNDF, ale pre realizaciu s NAND potrebujeme MNKF.
To dokazeme pomocou dvojitej negacie.
f = a + b'c + cd'
f'' = ((a'.(b'c)').(cd')')'
0. uroven: a, b, c, d
1. uroven: a', b', c, d'
2. uroven: a', (b'c)', (cd')'
3. uroven: vstup do hradla: a', (b'c)', (cd')'
Realizacia pomocou hradiel NOR
f(d,c,b,a) = b(a' + c)(c' + d)
f''(d,c,b,a) = (b' + (a' + c)' + (c' + d)')'
Pravidlo pre realizciu pomocou NOR znie: pre realizaciu logickych operacii + a . pouzivame hradlo NOR a to tak, ze premenne vstupujuce priamo do hradla na neparnej urovni od konca musia byt negovane.
A namiesto pocitania pomocou De Morganovych zakonov sme v oboch pripadoch mohli pouzit Rottove mriezky.
Literatura
http://www.electronics-tutorials.ws/combination/comb_1.html
HW 1.2 Minimalizacia vyrazov
Minule sme zistili, co su logicke funkcie a ako ich popisujeme. Dnes sa pozrieme na to, ako ich minimalizovat a co ta minimalizacia vlastne znamena.
Co je to minimalizacia logickej funkcie?
Tento pojem krasne vysvetluje pani docentka Kubatova vo svojich skriptach. Pri minimalizacii sledujeme jediny ciel a tym je "najst co najjednoduchsie vyjadrenie logickej funkcie". Otazkou zostava, co znamena najjednoduchsie vyjadrenie. Aj na tuto otazku nam skripta poskytuju odpoved. Jedna sa o take vyjadrenie funkcie, ktore obsahuje
Minimalna normalova disjunktivna forma, dalej MNDF je logicky sucet minimalneho poctu minimalnych P-termov
Minimalna normalova konjuktivna forma, dalej MNKF je logicky sucin minimalneho poctu minimalnych S-termov
Co je P-term a S-term sme pisali uz minule, ale mozno sa hodi to trosku zopakovat (kto by si to vsetko pamatal, ze?).
P-term, alebo sucinovy term, je vyraz (term) tvoreny len premennymi a operaciami logickeho sucinu
S-term, alebo suctovy term, je term tvoreny len premennymi a operaciami logickeho suctu
Minterm je taky P-term, ktory obsahuje vsetky nezavisle premenne
Maxterm je taky S-term, ktory obsahuje vsetky nezavisle premenne
Preklad definicie MNDF/MNKF je teda taky, ze sa jedna o sucet/sucin co najmensieho poctu P/S-termov, ktore obsahuju co najmensi pocet premennych a negovanych premennych. To vlastne aj pasuje k "definicii" jednoduchosti vyjadrenia fcie.
Ako minimalizovat?
Huraa :), mozme sa vrhnut na minimalizaciu :). Mame na vyber viacero sposobov (a vsetky je dobre vediet). Minimalizovat mozme pomocou:
Ako nazov naznacuje, jedna sa o sposob minimalizacie pomocou zakladnych a odvodenych zakonov Boolovej algebry. Takze upravujeme funkciu, az kym ju nezminimalizujeme natolko, ze uz dalej to nejde :). K tomu sa jedine da dodat, ze sa pozrite na zakony boolovej algebry a skuste si vypocitat par prikladov. Lepsia cesta snad neexistuje. Inak, toto je celkom odbre opakovanie boolovej algebry, bez ktorej to proste nejde ;). Este jeden detail, v boolovej algebre ma bin. sucin aj bin. sucet rovnaku prioritu, takze bacha na zapis. Moj zapis bude vacsinou zodpovedat pravidlam z algebry realnych cisel (najprv nasobim, potom scitam ... )
Priklad (overit prebraty zo studentskeho servru):
¬(a + b) + a + ab
¬(a + b) + a . (1 + b) {distributivita}
¬(a + b) + a . 1 {agresivita 1 vzhledem ke sčítání}
¬(a + b) + a {neutralita 1 vzhledem k násobení}
¬a . ¬b + a {deMorganův zákon}
b + a {absorbce negace}
Minimalizacia pomocou map
Minimalizacia pomocou map je peknou nazornou metodou minimalizacie. Pouzivat budem Karnaughovu mapu, pretoze je vytvorena tak, aby susedne stavy boli topologicky vedla seba. Na obrazku znazorneny susedny stav pre s=10 pre Karnaughovu/Svobodovu mapu (v poradi).
Ako budeme postupovat:
Dobre si vsimnite, aky je rozdiel medzi popisovaninm MNDF a MNKF == dobre prestudujte obrazok!
MNKF: (a' + b') . (a + b + c) . (a + c + d)
MNDF: ab' + a'c + a'bd
Este jeden pekny obrazok map s popisom fcii:
Quine-McCluskey
Tato metoda bola vyvinuta pre pouzitie na cislicovych pocitacoch a pre minimalizaciu logickych funkcii vacsieho poctu nezavislych premennych.
f(d,c,b,a) = SUM(1,4,7,8,9,10,11,12,14,15)
spravime pravdivostnu tabulku:
s d c b a | f(d,c,b,a)
0 0 0 0 0 0
1 0 0 0 1 1
2 0 0 1 0 0
3 0 0 1 1 0
4 0 1 0 0 1
5 0 1 0 1 0
6 0 1 1 0 0
7 0 1 1 1 1
8 1 0 0 0 1
9 1 0 0 1 1
10 1 0 1 0 1
11 1 0 1 1 1
12 1 1 0 0 1
13 1 1 0 1 0
14 1 1 1 0 1
15 1 1 1 1 1
vyberieme si len jednickove stavy, pretoze len s nimi budeme pracovat. V tychto stavoch musime vyhladat a "zgrupit" jednotkove stavy.
1. stavy zoradime podla poctu jedniciek
2. najdeme susedne dovjice medzi skupinami z bodu 1, ale popiseme ich len 3 premennymi. (susedne dvojice sa zhoduju v jednej jednicke a odlisne su v jednom stave)
3. najdeme susedne dvojice
4. najdeme stavy/skupiny, ktore nie su pokryte ziadnou vacsou skupinou stavov - oznacime velkym pismenom a tieto skupiny budu oznacovat priame implikanty funkcie f(d,c,b,a)
Povodne Podla n 1iek Susedne 2ice Susedne 4ice
d c b a | s | d c b a | s | d c b a | s | d c b a | s
0 0 0 1 1 | 0 0 0 1 | 1 | - 0 0 1 | 1,9 F |
0 1 0 0 4 | 0 1 0 0 | 4 | - 1 0 0 | 4,12 E | 1 - - 0 | 8,10,12,14
0 1 1 1 7 | 1 0 0 0 | 8 | 1 0 - 0 | 8,10 | 1 0 - - | 8,10,9,11
| 1 0 0 - | 8,9 | 1 0 - - | 8, 9, 10, 11 C
| 1 - 0 0 | 8,12 | 1 - - 0 | 8,12,10,14 B
1 0 0 0 8 | 1 0 0 1 | 9 | 1 0 - 1 | 9,11 |
1 0 0 1 9 | 1 0 1 0 | 10 | 1 0 1 - | 10,11 | 1 - 1 - | 10,11,14,15 A
| 1 - 1 0 | 10,14 | 1 - 1 - | 10,14,11,15
1 0 1 0 10 | 1 1 0 0 | 12 | 1 1 - 0 | 12,14 |
1 0 1 1 11 | 0 1 1 1 | 7 | - 1 1 1 | 7,15 D |
1 1 0 0 12 | 1 0 1 1 | 11 | 1 - 1 1 | 11,15 |
1 1 1 0 14 | 1 1 1 0 | 14 | 1 1 1 - | 14,15 |
1 1 1 1 15 | 1 1 1 1 | 15 | |
Z tohto pocinu vyssie musime najst MNDF. A aby to nebolo tak jednoduche, tak budeme potrebovat dalsiu tabulku a to tabulku pokrytia.Tabulka pokryva vsetky jednickove stavy a obsahuje minimalny pocet prvkov.
1 4 7 8 9 10 11 12 14 15
A bd * * * *
B a'd * * * *
C c'd * * * *
D abc * *
E a'b'c * *
F ab'c' * *
V tabulke pokrytia * oznacuje, z ktorych stavov je dany implikant tvoreny.
Uff, :). Good Luck! :)
Pouzita literatura
[1] Logicke obvody, Kubatova, FEL CVUT Praha - velmi pekne napisane skripta, doporucujem do nich mrknut, ak nieco nie je jasne.
Co je to minimalizacia logickej funkcie?
Tento pojem krasne vysvetluje pani docentka Kubatova vo svojich skriptach. Pri minimalizacii sledujeme jediny ciel a tym je "najst co najjednoduchsie vyjadrenie logickej funkcie". Otazkou zostava, co znamena najjednoduchsie vyjadrenie. Aj na tuto otazku nam skripta poskytuju odpoved. Jedna sa o take vyjadrenie funkcie, ktore obsahuje
- minimalny pocet termov
- minimalny pocet nezavisle premennych v kazdom terme
- minimalny pocet negovanych premennych
Minimalna normalova disjunktivna forma, dalej MNDF je logicky sucet minimalneho poctu minimalnych P-termov
Minimalna normalova konjuktivna forma, dalej MNKF je logicky sucin minimalneho poctu minimalnych S-termov
Co je P-term a S-term sme pisali uz minule, ale mozno sa hodi to trosku zopakovat (kto by si to vsetko pamatal, ze?).
P-term, alebo sucinovy term, je vyraz (term) tvoreny len premennymi a operaciami logickeho sucinu
S-term, alebo suctovy term, je term tvoreny len premennymi a operaciami logickeho suctu
Minterm je taky P-term, ktory obsahuje vsetky nezavisle premenne
Maxterm je taky S-term, ktory obsahuje vsetky nezavisle premenne
Preklad definicie MNDF/MNKF je teda taky, ze sa jedna o sucet/sucin co najmensieho poctu P/S-termov, ktore obsahuju co najmensi pocet premennych a negovanych premennych. To vlastne aj pasuje k "definicii" jednoduchosti vyjadrenia fcie.
Ako minimalizovat?
Huraa :), mozme sa vrhnut na minimalizaciu :). Mame na vyber viacero sposobov (a vsetky je dobre vediet). Minimalizovat mozme pomocou:
- boolovej algebry
- mapy
- metody Quine-McCluskey
Ako nazov naznacuje, jedna sa o sposob minimalizacie pomocou zakladnych a odvodenych zakonov Boolovej algebry. Takze upravujeme funkciu, az kym ju nezminimalizujeme natolko, ze uz dalej to nejde :). K tomu sa jedine da dodat, ze sa pozrite na zakony boolovej algebry a skuste si vypocitat par prikladov. Lepsia cesta snad neexistuje. Inak, toto je celkom odbre opakovanie boolovej algebry, bez ktorej to proste nejde ;). Este jeden detail, v boolovej algebre ma bin. sucin aj bin. sucet rovnaku prioritu, takze bacha na zapis. Moj zapis bude vacsinou zodpovedat pravidlam z algebry realnych cisel (najprv nasobim, potom scitam ... )
Priklad (overit prebraty zo studentskeho servru):
¬(a + b) + a + ab
¬(a + b) + a . (1 + b) {distributivita}
¬(a + b) + a . 1 {agresivita 1 vzhledem ke sčítání}
¬(a + b) + a {neutralita 1 vzhledem k násobení}
¬a . ¬b + a {deMorganův zákon}
b + a {absorbce negace}
Minimalizacia pomocou map
Minimalizacia pomocou map je peknou nazornou metodou minimalizacie. Pouzivat budem Karnaughovu mapu, pretoze je vytvorena tak, aby susedne stavy boli topologicky vedla seba. Na obrazku znazorneny susedny stav pre s=10 pre Karnaughovu/Svobodovu mapu (v poradi).
Ako budeme postupovat:
- funkciu zapiseme do mapy
- budeme si vsimat susedne stavy a hladat vzdy najvacsiu skupinu (vzdy 2^n stavov)
- 1cky ak hladame MNDF
- 0ky ak hladame MNKF
- plati, ze cim vacsia skupina susendych stavov, tym mensi pocet nezavisle premennych potrebujeme k popisu
- vyberieme skupiny, ktore zodpovedaju kriteriu minimality
MNKF: (a' + b') . (a + b + c) . (a + c + d)
MNDF: ab' + a'c + a'bd
Este jeden pekny obrazok map s popisom fcii:
Quine-McCluskey
Tato metoda bola vyvinuta pre pouzitie na cislicovych pocitacoch a pre minimalizaciu logickych funkcii vacsieho poctu nezavislych premennych.
f(d,c,b,a) = SUM(1,4,7,8,9,10,11,12,14,15)
spravime pravdivostnu tabulku:
s d c b a | f(d,c,b,a)
0 0 0 0 0 0
1 0 0 0 1 1
2 0 0 1 0 0
3 0 0 1 1 0
4 0 1 0 0 1
5 0 1 0 1 0
6 0 1 1 0 0
7 0 1 1 1 1
8 1 0 0 0 1
9 1 0 0 1 1
10 1 0 1 0 1
11 1 0 1 1 1
12 1 1 0 0 1
13 1 1 0 1 0
14 1 1 1 0 1
15 1 1 1 1 1
vyberieme si len jednickove stavy, pretoze len s nimi budeme pracovat. V tychto stavoch musime vyhladat a "zgrupit" jednotkove stavy.
1. stavy zoradime podla poctu jedniciek
2. najdeme susedne dovjice medzi skupinami z bodu 1, ale popiseme ich len 3 premennymi. (susedne dvojice sa zhoduju v jednej jednicke a odlisne su v jednom stave)
3. najdeme susedne dvojice
4. najdeme stavy/skupiny, ktore nie su pokryte ziadnou vacsou skupinou stavov - oznacime velkym pismenom a tieto skupiny budu oznacovat priame implikanty funkcie f(d,c,b,a)
Povodne Podla n 1iek Susedne 2ice Susedne 4ice
d c b a | s | d c b a | s | d c b a | s | d c b a | s
0 0 0 1 1 | 0 0 0 1 | 1 | - 0 0 1 | 1,9 F |
0 1 0 0 4 | 0 1 0 0 | 4 | - 1 0 0 | 4,12 E | 1 - - 0 | 8,10,12,14
0 1 1 1 7 | 1 0 0 0 | 8 | 1 0 - 0 | 8,10 | 1 0 - - | 8,10,9,11
| 1 0 0 - | 8,9 | 1 0 - - | 8, 9, 10, 11 C
| 1 - 0 0 | 8,12 | 1 - - 0 | 8,12,10,14 B
1 0 0 0 8 | 1 0 0 1 | 9 | 1 0 - 1 | 9,11 |
1 0 0 1 9 | 1 0 1 0 | 10 | 1 0 1 - | 10,11 | 1 - 1 - | 10,11,14,15 A
| 1 - 1 0 | 10,14 | 1 - 1 - | 10,14,11,15
1 0 1 0 10 | 1 1 0 0 | 12 | 1 1 - 0 | 12,14 |
1 0 1 1 11 | 0 1 1 1 | 7 | - 1 1 1 | 7,15 D |
1 1 0 0 12 | 1 0 1 1 | 11 | 1 - 1 1 | 11,15 |
1 1 1 0 14 | 1 1 1 0 | 14 | 1 1 1 - | 14,15 |
1 1 1 1 15 | 1 1 1 1 | 15 | |
Z tohto pocinu vyssie musime najst MNDF. A aby to nebolo tak jednoduche, tak budeme potrebovat dalsiu tabulku a to tabulku pokrytia.Tabulka pokryva vsetky jednickove stavy a obsahuje minimalny pocet prvkov.
1 4 7 8 9 10 11 12 14 15
A bd * * * *
B a'd * * * *
C c'd * * * *
D abc * *
E a'b'c * *
F ab'c' * *
V tabulke pokrytia * oznacuje, z ktorych stavov je dany implikant tvoreny.
- Najdeme stlpce, ktore obsahuju len jednu hviezdicku. V tomto pripade to je 1,4,7 a nalezia implikantom D,E,F. Tieto implikanty nazyvame nesporne priame implikanty.
- V riadku, ktory patri k nespornemu implikantu, vyskrtneme stlpce, ktore obsahuju hviezdicku
8 10 11 14
A bd * * *
B a'd * * *
C c'd * * *
- S takto upravenou tabulkou zopakujeme bod 1 a 2
- Najdeme taky stav, ze ostatne stavy su jeho podmnozinou. V tomto pripade 10, pretoze pokryva stavy, ktore pokryvaju stavy 8, 11, 14. 10 teda mozme vyskrtnut. Budeme to volat dominancia stlpcov.
8 11 14
A bd * *
B a'd * *
C c'd * * - Dominancia riadkov. Hladame teda riadok taky, ze niektory z dalsich riadkov je jeho podmnozinou. Taky stlpec v tabulke nie je.
8 11 14
A bd * *
B a'd * *
C c'd * * - A konecne vyberieme termy. Nesmieme zabudnut pouzit nesporne priame implikanty z bodu 1!
f(d,c,b,a) = abc + a'b'c + ab'c' + bd + c'd alebo
f(d,c,b,a) = abc + a'b'c + ab'c' + bd + a'd
moznost a'd + c'd sme nepouzili, aby sme co najviac uspokojili kriterium minimality.
Uff, :). Good Luck! :)
Pouzita literatura
[1] Logicke obvody, Kubatova, FEL CVUT Praha - velmi pekne napisane skripta, doporucujem do nich mrknut, ak nieco nie je jasne.
Saturday, May 7, 2011
HW.1.1 Logické funkce a formy jejich popisu
1. Co su logicke funkcie
2. Ake su formy popisu logickych funkcii
Aby sme mohli zacar s logickymi funkciami, musime si najprv uvedomit, k comu sluzia a co to tie logicke funkcie vlastne su.Pre tych, co uz zabudli Boolovu algebru, odporucam si ju zopakovat ;).
Funkce definovane na n-ticiach vytvorenych z prvkov z mnoziny {0,1} zobrazenych do mnoziny {0,1} sa nazyvaju Boolovymi funckiami n argumentov. V rovnakom vyzname sa casto pouziva termin logicka funkcia. Pre vyjadrenie logickych funkcii je mozne pouzit niekolko rozdielnych pristupov - slovny popis, algebraicky vyraz, tabulku, mapu, jednotkovu kocku. [1] . Pri zapise log. f. budeme pouzivat ' namiesto negace, teda a' == NOT(a).
Prikladom logickej funkcie moze byt a`.b + a.c` + b.c. {F1}
Jednu a tu istu funkciu je mozne zadat viacerymi Boolovskymi vyrazmi a preto pouzivame standardny tvar, ktory nazyvame normalova forma alebo kanonicky tvar. Jedna sa o take vyjadrenie funkcie, kde sa vyskytuju operacie logickeho sucinu a logickeho suctu iba na dvoch urovniach. Napriklad vyssie uvedena F1 alebo napriklad (a+b).(a+b'+c') {F2}. Normalizaciou sa budeme zaoberat v nadvazujucom clanku.
Pre popis logickych funckii mozeme vuyzit viacero metod. Niektore z nich si uvedieme, ale najprv absolvujeme neprijemnu cast. Troska terminlogie, ktora bude uzitocna pre dalsi vyklad:
Term je vyraz tvoreny len premennymi a operaciami logickeho suctu a sucinu [1]
P-term, alebo sucinovy term, je vyraz (term) tvoreny len premennymi a operaciami logickeho sucinu [1]
S-term, alebo suctovy term, je term tvoreny len premennymi a operaciami logickeho suctu [1]
Minterm je taky P-term, ktory obsahuje vsetky nezavisle premenne [1]
Maxterm je taky S-term, ktory obsahuje vsetky nezavisle premenne [1]
Stavovy index je desiatkovy zapis kombinacie hodnot nezavisle premennych [1]
Vstupne pismeno je kombinacia hodnot vstupnnych premennych [1]
Kazda logicka funkcia moze pozostavat zo suctu mintermov (napr. F1 vyssie) alebo sucinu maxtermov (napr. vyssie uvedena F2). Ak pocet vstupny premennych je n, tak mozme vytvorit 2^n mintermov alebo maxtermov, kde kazdy min/maxterm nadobuda logicku hodnotu (1/0) prave pre jedine vstupne pismeno logickej funkcie [1]
UNDF oznacuje uplne normalovu disjunktivnu formu a jedna sa o logicky vyraz tvoreny suctom mintermov. Mozme pouzit vsetky mintermy, alebo pouzijeme len tie, pre ktore logicka funkcia nadobuda hodnoty log. 1. [1]
UNKF oznacuje uplne normalovu konjuktivnu formu. Tu sa teda na rozdiel od UNDF jedna o log. Fciu tvorenu sucinom maxtermov, ale len tych ktore nenadobudaju hodnotu log. 1. [1].
Doporucujem mrknut na priklad nizsie, kde tvorime a mintermy a maxtermy z vyctu stavovych indexov a uplne idealne bude, ak si nieco z tychto prikladov spocitate ;).
Oba tieto zapisy su ekvivalentne. Ja radsej pouzivam UNDF (pretoze si nikdy neviem zvyknut ze tam, kde je 1 mam pri UNKF pouzit negaciu .. ) a preto budem pouzivat prave tuto formu zapisu, pokial nie je nutne inak.
Popis logickych funkcii
Pravdivostne tabulky
Pomocou pravdivostnej tabulky je mozne vyjadrit kazdu logicku funkciu.
Stavovy index s cba f(c,b,a) minterm Ps maxterm Ss
0 000 0 c'b'a' c + b + a
1 001 1 c'b'a c + b + a'
2 010 1 c'ba' c + b' + a
3 011 0 c'ba c + b' + a'
4 100 1 cb'a' c' + b + a
5 101 0 cb'a c' + b + a'
6 110 1 cba' c' + b' + a
7 111 0 cba c' + b' + a'
Doporucujem si pozriet aj pravdivostnu tabulku v nizsie uvedenom priklade scitacky.
Mapy
Mapy su jednou z moznosti, ako vyjadrit logicku funkciu. Mapa je plosny utvar, ktory je rozdeleny do 2^n poli, kde n je pocet nezavislych premennych logickej fcie [1]. Jedna sa teda o dvojrozmerne pole m . n, kde m aj n je mocnina 2. Podla vzajomneho priradenia policka k stavovym indexom rozdelujeme mapy na Karnaughovu mapu a Svobodovu mapu (postacuju pre nase potreby).Su vhodnym prostriedkom pre vyjadrenie log. fcii a pre minimalizaciu fcii 2 - 6 premennych.
Svobodova Mapa
Svobodova mapa najviac zodpoveda pravdivostnej tabulke. Stavove indexy su zoradene do policok, ktore nasleduju vedla seba. Ak niekde budete pocut nazov Veitchova alebo Marquandova, tak autor mal na mysli prave tuto mapu.
Karnaughova mapa
V buducnosti sa budeme zaoberat minimalizaciou logickej funkcie a pre tieto potreby sa nam viac hodi prave Karnaughova mapa. Do policok sa vzdy zapisu susedne stavy, teda kombinacie hodnot nezavislych premennych zobrazenych do policok vedla seba, sa lisia vzdy hodnotou jednej nezavislej premennej [1].
Mapu mozme zaviest aj pomocou Grayovho kodu. V takomto pripade sa pri prechode medzi susednymi stavmi bude vzdy menit len jedna premenna. Grayov kod a Karnaughova mapa s jeho vyuzitim su znazornene na obrazky nizsie.
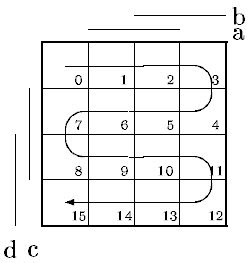
Priklad: f(d,c,b,a) = SUM(1,2,4,6,9,11,15). Znamena to, ze jednotky zapiseme do policok so stavovym indexom, ako na pravej casti fcie.
Pri viacerych nezavislych premennych zvacsujeme pocet riadkov, ziskame nove riadky posunutim u Svobodovej mapy a otocenim u Karnaughovej mapy.
Jednotkova kocka
Toto vyjadrenie nie je velmi nazorne a nebudeme ho pouzivat, ale slubujem, ze sa k nemu vratim a doplnim hned, ako sa dostanem k nejakemu plnohodnotnemu vyjadreniu :).
Dalsie moznosti su formy popisu logickym vyrazom a zoznamom indexov vstupnych pismen.
Formy popisu by sme mali, na tomto mieste by vsak bolo vhodne uviest si nejaky priklad, aby bolo uplne jasne o co tu vlastne ide. Uz sme uviedli, ze mapy budeme s vyhodou pouzivat pri minimalizacii logickych funkcii. Nikde sme vsak neuviedli, ako sa vlastne k takej mape dostaneme.
Priklad
Ako priklad si vyberieme scitacku. Vytvorime mapu, vyjadrime log. fcie a v dalsej kapitole si ukazeme, ako ich zminimalizujeme.
Scitacka si v tejto chvili predstavime ako black box. Na scitanie potrebujem dvoch scitancov. Vystupom je vysledok scitania. Urcite Vas napadlo, ze sa s tymto riesenim dostaneme do problemov, ak cisla budu dost velke na to, ze budeme potrebovat dalsi vstup, ktory bude sluzit ako prenos.
Teda, vstupom budu 3 premenne, a, b a p. Vystupom bude q a s, kde q bude vstupom pre dalsi prenos a s je vysledkom.
st. index a b p q s
0 1 1 1 | 1 1
1 1 1 0 | 1 0
2 1 0 1 | 1 0
3 1 0 0 | 0 1
4 0 1 1 | 1 0
5 0 1 0 | 0 1
6 0 0 1 | 0 1
7 0 0 0 | 0 0
Z pravdivostnej tabulky dostaneme nasledujuce logicke funkcie:
S = abp + ab’p‘ + a’bp‘ + a’b‘p
Q = abp + abp‘ + ab’p + a’bp
Vsimnite si, ze zapis je tvoreny suctom mintermov. Jedna sa teda o UNDF.
Ak by sme chceli pouzit UNKF, tak by nas vysledok vyzeral takto:
S = (a+b+p) . (ab’p‘) . (a‘ + b + p) . (a’ + b + p‘) . (a’ + b‘ + p)
Q = (a’+b’+p) . (a’+b+p‘) . (a+b’+p‘) . (a+b+p)
Priklad
f(c,b,a) = SUM(0,1,5,6,7) (teda vycet stavovych indexov, kde f nadobuda log. hodnoty 1)
Aby sme si to vedeli predstavit, tak si vypiseme pravdivostnu tabulku. Vsimnite si, ako priradujeme hodnoty jednotlivym premennym, ak sa na chvilku zamyslite, tak Vam to isto da logiku J.
s c b a f(c,b,a)
0 0 0 0 1
1 0 0 1 1
2 0 1 0 0
3 0 1 1 0
4 1 0 0 0
5 1 0 1 1
6 1 1 0 1
7 1 1 1 1
UNDF: z vyssie uvedenj definice vyplyva, ze pouzijeme vsetky mintermy, alebo len tie, kde f(c,b,a) nadobuda log. 1. A kedze clovek je tvor lenivy a my nie sme vynimky, tak vypiseme len tie mintermi, kde fcie nadobudne 1.
c’b’a‘ + c’b’a + cb’a + cba‘ + cba
UNKF: opat hodime okom na vyssie uvedenu fciu a zistime, ze pouzijeme maxtermy, ale len tie, ktore nenadobudaju hodnotu log. 1. Pouzijeme teda sposob, ako pri UNDF s „mensimi“ odchylkami.
(c+b’+a) . (c+b’+a‘) . (c’+b+a)
Karnaughova mapa
Takto vyzera Karnaughova mapa, v ktorej su zapisane stavove indexy. Vsimnite si, ako koresponduje s pravidvostnou tabulkou. Napriklad pre s = 0 su hodnoty premennych a,b,c = 0 ako v tabulke, tak v mape.
A takto vyzera ked je vyplnena. Ak porovnate mapu vyssie (tu s tymi farebnymi ciarami J ) a nasledujucu mapu a pravdivostnu tabulku, tak urcite zistite, ze lahsie to uz snad byt nemoze J.
Svobodova mapa
Tiez nic zloziteho, ale davajte si pozor na rozlisne priradenie stavovych indexov k jednotlivym polickam mapy. Ak to spachate zle, tak vam to nebude sediet.
------------- b
--- --- a
tabulku vyplnime:
------------ b
--- --- a
Priklad
f(c,b,a) = PI(1,2,5,6) (teda vycet stavovych indexov, kde f nadobuda log. hodnoty 0)
s c b a f(c,b,a)
0 0 0 0 1
1 0 0 1 0
2 0 1 0 0
3 0 1 1 1
4 1 0 0 1
5 1 0 1 0
6 1 1 0 0
7 1 1 1 1
Karnaughova mapa:
------------- b
------------ a
1 0 1 0
c | 1 0 0 1
Svobodova mapa:
--------------b
--- --- a
1 0 0 0
c | 1 1 0 1
UNKF: (a' + b + c) . (a + b' + c) . (a' + b + c') . (a + b' + c')
UNDF: a'b'c' + abc' + a'b'c + abc
Good luck ;)
Pouzita literatura:
[1] Logicke obvody, Kubatova, FEL CVUT Praha
2. Ake su formy popisu logickych funkcii
Aby sme mohli zacar s logickymi funkciami, musime si najprv uvedomit, k comu sluzia a co to tie logicke funkcie vlastne su.Pre tych, co uz zabudli Boolovu algebru, odporucam si ju zopakovat ;).
Funkce definovane na n-ticiach vytvorenych z prvkov z mnoziny {0,1} zobrazenych do mnoziny {0,1} sa nazyvaju Boolovymi funckiami n argumentov. V rovnakom vyzname sa casto pouziva termin logicka funkcia. Pre vyjadrenie logickych funkcii je mozne pouzit niekolko rozdielnych pristupov - slovny popis, algebraicky vyraz, tabulku, mapu, jednotkovu kocku. [1] . Pri zapise log. f. budeme pouzivat ' namiesto negace, teda a' == NOT(a).
Prikladom logickej funkcie moze byt a`.b + a.c` + b.c. {F1}
Jednu a tu istu funkciu je mozne zadat viacerymi Boolovskymi vyrazmi a preto pouzivame standardny tvar, ktory nazyvame normalova forma alebo kanonicky tvar. Jedna sa o take vyjadrenie funkcie, kde sa vyskytuju operacie logickeho sucinu a logickeho suctu iba na dvoch urovniach. Napriklad vyssie uvedena F1 alebo napriklad (a+b).(a+b'+c') {F2}. Normalizaciou sa budeme zaoberat v nadvazujucom clanku.
Pre popis logickych funckii mozeme vuyzit viacero metod. Niektore z nich si uvedieme, ale najprv absolvujeme neprijemnu cast. Troska terminlogie, ktora bude uzitocna pre dalsi vyklad:
Term je vyraz tvoreny len premennymi a operaciami logickeho suctu a sucinu [1]
P-term, alebo sucinovy term, je vyraz (term) tvoreny len premennymi a operaciami logickeho sucinu [1]
S-term, alebo suctovy term, je term tvoreny len premennymi a operaciami logickeho suctu [1]
Minterm je taky P-term, ktory obsahuje vsetky nezavisle premenne [1]
Maxterm je taky S-term, ktory obsahuje vsetky nezavisle premenne [1]
Stavovy index je desiatkovy zapis kombinacie hodnot nezavisle premennych [1]
Vstupne pismeno je kombinacia hodnot vstupnnych premennych [1]
Kazda logicka funkcia moze pozostavat zo suctu mintermov (napr. F1 vyssie) alebo sucinu maxtermov (napr. vyssie uvedena F2). Ak pocet vstupny premennych je n, tak mozme vytvorit 2^n mintermov alebo maxtermov, kde kazdy min/maxterm nadobuda logicku hodnotu (1/0) prave pre jedine vstupne pismeno logickej funkcie [1]
UNDF oznacuje uplne normalovu disjunktivnu formu a jedna sa o logicky vyraz tvoreny suctom mintermov. Mozme pouzit vsetky mintermy, alebo pouzijeme len tie, pre ktore logicka funkcia nadobuda hodnoty log. 1. [1]
UNKF oznacuje uplne normalovu konjuktivnu formu. Tu sa teda na rozdiel od UNDF jedna o log. Fciu tvorenu sucinom maxtermov, ale len tych ktore nenadobudaju hodnotu log. 1. [1].
Doporucujem mrknut na priklad nizsie, kde tvorime a mintermy a maxtermy z vyctu stavovych indexov a uplne idealne bude, ak si nieco z tychto prikladov spocitate ;).
Oba tieto zapisy su ekvivalentne. Ja radsej pouzivam UNDF (pretoze si nikdy neviem zvyknut ze tam, kde je 1 mam pri UNKF pouzit negaciu .. ) a preto budem pouzivat prave tuto formu zapisu, pokial nie je nutne inak.
Popis logickych funkcii
Pravdivostne tabulky
Pomocou pravdivostnej tabulky je mozne vyjadrit kazdu logicku funkciu.
Stavovy index s cba f(c,b,a) minterm Ps maxterm Ss
0 000 0 c'b'a' c + b + a
1 001 1 c'b'a c + b + a'
2 010 1 c'ba' c + b' + a
3 011 0 c'ba c + b' + a'
4 100 1 cb'a' c' + b + a
5 101 0 cb'a c' + b + a'
6 110 1 cba' c' + b' + a
7 111 0 cba c' + b' + a'
Doporucujem si pozriet aj pravdivostnu tabulku v nizsie uvedenom priklade scitacky.
Mapy
Mapy su jednou z moznosti, ako vyjadrit logicku funkciu. Mapa je plosny utvar, ktory je rozdeleny do 2^n poli, kde n je pocet nezavislych premennych logickej fcie [1]. Jedna sa teda o dvojrozmerne pole m . n, kde m aj n je mocnina 2. Podla vzajomneho priradenia policka k stavovym indexom rozdelujeme mapy na Karnaughovu mapu a Svobodovu mapu (postacuju pre nase potreby).Su vhodnym prostriedkom pre vyjadrenie log. fcii a pre minimalizaciu fcii 2 - 6 premennych.
Svobodova Mapa
Svobodova mapa najviac zodpoveda pravdivostnej tabulke. Stavove indexy su zoradene do policok, ktore nasleduju vedla seba. Ak niekde budete pocut nazov Veitchova alebo Marquandova, tak autor mal na mysli prave tuto mapu.
Karnaughova mapa
V buducnosti sa budeme zaoberat minimalizaciou logickej funkcie a pre tieto potreby sa nam viac hodi prave Karnaughova mapa. Do policok sa vzdy zapisu susedne stavy, teda kombinacie hodnot nezavislych premennych zobrazenych do policok vedla seba, sa lisia vzdy hodnotou jednej nezavislej premennej [1].
Mapu mozme zaviest aj pomocou Grayovho kodu. V takomto pripade sa pri prechode medzi susednymi stavmi bude vzdy menit len jedna premenna. Grayov kod a Karnaughova mapa s jeho vyuzitim su znazornene na obrazky nizsie.
Priklad: f(d,c,b,a) = SUM(1,2,4,6,9,11,15). Znamena to, ze jednotky zapiseme do policok so stavovym indexom, ako na pravej casti fcie.
Pri viacerych nezavislych premennych zvacsujeme pocet riadkov, ziskame nove riadky posunutim u Svobodovej mapy a otocenim u Karnaughovej mapy.
Toto vyjadrenie nie je velmi nazorne a nebudeme ho pouzivat, ale slubujem, ze sa k nemu vratim a doplnim hned, ako sa dostanem k nejakemu plnohodnotnemu vyjadreniu :).
Dalsie moznosti su formy popisu logickym vyrazom a zoznamom indexov vstupnych pismen.
Formy popisu by sme mali, na tomto mieste by vsak bolo vhodne uviest si nejaky priklad, aby bolo uplne jasne o co tu vlastne ide. Uz sme uviedli, ze mapy budeme s vyhodou pouzivat pri minimalizacii logickych funkcii. Nikde sme vsak neuviedli, ako sa vlastne k takej mape dostaneme.
Priklad
Ako priklad si vyberieme scitacku. Vytvorime mapu, vyjadrime log. fcie a v dalsej kapitole si ukazeme, ako ich zminimalizujeme.
Scitacka si v tejto chvili predstavime ako black box. Na scitanie potrebujem dvoch scitancov. Vystupom je vysledok scitania. Urcite Vas napadlo, ze sa s tymto riesenim dostaneme do problemov, ak cisla budu dost velke na to, ze budeme potrebovat dalsi vstup, ktory bude sluzit ako prenos.
Teda, vstupom budu 3 premenne, a, b a p. Vystupom bude q a s, kde q bude vstupom pre dalsi prenos a s je vysledkom.
st. index a b p q s
0 1 1 1 | 1 1
1 1 1 0 | 1 0
2 1 0 1 | 1 0
3 1 0 0 | 0 1
4 0 1 1 | 1 0
5 0 1 0 | 0 1
6 0 0 1 | 0 1
7 0 0 0 | 0 0
Z pravdivostnej tabulky dostaneme nasledujuce logicke funkcie:
S = abp + ab’p‘ + a’bp‘ + a’b‘p
Q = abp + abp‘ + ab’p + a’bp
Vsimnite si, ze zapis je tvoreny suctom mintermov. Jedna sa teda o UNDF.
Ak by sme chceli pouzit UNKF, tak by nas vysledok vyzeral takto:
S = (a+b+p) . (ab’p‘) . (a‘ + b + p) . (a’ + b + p‘) . (a’ + b‘ + p)
Q = (a’+b’+p) . (a’+b+p‘) . (a+b’+p‘) . (a+b+p)
Priklad
f(c,b,a) = SUM(0,1,5,6,7) (teda vycet stavovych indexov, kde f nadobuda log. hodnoty 1)
Aby sme si to vedeli predstavit, tak si vypiseme pravdivostnu tabulku. Vsimnite si, ako priradujeme hodnoty jednotlivym premennym, ak sa na chvilku zamyslite, tak Vam to isto da logiku J.
s c b a f(c,b,a)
0 0 0 0 1
1 0 0 1 1
2 0 1 0 0
3 0 1 1 0
4 1 0 0 0
5 1 0 1 1
6 1 1 0 1
7 1 1 1 1
UNDF: z vyssie uvedenj definice vyplyva, ze pouzijeme vsetky mintermy, alebo len tie, kde f(c,b,a) nadobuda log. 1. A kedze clovek je tvor lenivy a my nie sme vynimky, tak vypiseme len tie mintermi, kde fcie nadobudne 1.
· Z tabulky vyberieme len riadky, kde f(c,b,a) = 1
· Jedna sa mintermy, takze budeme tvorit sucin
· Kazdu premennu, ktora je rovna 0 znegujeme
· Kedze sa jedna o UNDF, tak medzi mintermami bude sucet
UNKF: opat hodime okom na vyssie uvedenu fciu a zistime, ze pouzijeme maxtermy, ale len tie, ktore nenadobudaju hodnotu log. 1. Pouzijeme teda sposob, ako pri UNDF s „mensimi“ odchylkami.
· Z tabulky vyberieme len riadky, kde f(c,b,a) = 0
· Jedna sa maxtermy, takze budeme tvorit sucet
· Kazdu premennu, ktora je rovna 1 znegujeme
· Kedze sa jedna o UNKF, tak medzi maxtermami bude sucin
(c+b’+a) . (c+b’+a‘) . (c’+b+a)
Karnaughova mapa
Takto vyzera Karnaughova mapa, v ktorej su zapisane stavove indexy. Vsimnite si, ako koresponduje s pravidvostnou tabulkou. Napriklad pre s = 0 su hodnoty premennych a,b,c = 0 ako v tabulke, tak v mape.
A takto vyzera ked je vyplnena. Ak porovnate mapu vyssie (tu s tymi farebnymi ciarami J ) a nasledujucu mapu a pravdivostnu tabulku, tak urcite zistite, ze lahsie to uz snad byt nemoze J.
---------- b
----------- a1 1 0 0
c| 0 1 1 1Svobodova mapa
Tiez nic zloziteho, ale davajte si pozor na rozlisne priradenie stavovych indexov k jednotlivym polickam mapy. Ak to spachate zle, tak vam to nebude sediet.
------------- b
--- --- a
0 1 2 3
c| 4 5 6 7tabulku vyplnime:
------------ b
--- --- a
1 1 0 0
c| 0 1 1 1Priklad
f(c,b,a) = PI(1,2,5,6) (teda vycet stavovych indexov, kde f nadobuda log. hodnoty 0)
s c b a f(c,b,a)
0 0 0 0 1
1 0 0 1 0
2 0 1 0 0
3 0 1 1 1
4 1 0 0 1
5 1 0 1 0
6 1 1 0 0
7 1 1 1 1
Karnaughova mapa:
------------- b
------------ a
1 0 1 0
c | 1 0 0 1
Svobodova mapa:
--------------b
--- --- a
1 0 0 0
c | 1 1 0 1
UNKF: (a' + b + c) . (a + b' + c) . (a' + b + c') . (a + b' + c')
UNDF: a'b'c' + abc' + a'b'c + abc
Good luck ;)
Pouzita literatura:
[1] Logicke obvody, Kubatova, FEL CVUT Praha
Subscribe to:
Posts (Atom)