2. Ake su formy popisu logickych funkcii
Aby sme mohli zacar s logickymi funkciami, musime si najprv uvedomit, k comu sluzia a co to tie logicke funkcie vlastne su.Pre tych, co uz zabudli Boolovu algebru, odporucam si ju zopakovat ;).
Funkce definovane na n-ticiach vytvorenych z prvkov z mnoziny {0,1} zobrazenych do mnoziny {0,1} sa nazyvaju Boolovymi funckiami n argumentov. V rovnakom vyzname sa casto pouziva termin logicka funkcia. Pre vyjadrenie logickych funkcii je mozne pouzit niekolko rozdielnych pristupov - slovny popis, algebraicky vyraz, tabulku, mapu, jednotkovu kocku. [1] . Pri zapise log. f. budeme pouzivat ' namiesto negace, teda a' == NOT(a).
Prikladom logickej funkcie moze byt a`.b + a.c` + b.c. {F1}
Jednu a tu istu funkciu je mozne zadat viacerymi Boolovskymi vyrazmi a preto pouzivame standardny tvar, ktory nazyvame normalova forma alebo kanonicky tvar. Jedna sa o take vyjadrenie funkcie, kde sa vyskytuju operacie logickeho sucinu a logickeho suctu iba na dvoch urovniach. Napriklad vyssie uvedena F1 alebo napriklad (a+b).(a+b'+c') {F2}. Normalizaciou sa budeme zaoberat v nadvazujucom clanku.
Pre popis logickych funckii mozeme vuyzit viacero metod. Niektore z nich si uvedieme, ale najprv absolvujeme neprijemnu cast. Troska terminlogie, ktora bude uzitocna pre dalsi vyklad:
Term je vyraz tvoreny len premennymi a operaciami logickeho suctu a sucinu [1]
P-term, alebo sucinovy term, je vyraz (term) tvoreny len premennymi a operaciami logickeho sucinu [1]
S-term, alebo suctovy term, je term tvoreny len premennymi a operaciami logickeho suctu [1]
Minterm je taky P-term, ktory obsahuje vsetky nezavisle premenne [1]
Maxterm je taky S-term, ktory obsahuje vsetky nezavisle premenne [1]
Stavovy index je desiatkovy zapis kombinacie hodnot nezavisle premennych [1]
Vstupne pismeno je kombinacia hodnot vstupnnych premennych [1]
Kazda logicka funkcia moze pozostavat zo suctu mintermov (napr. F1 vyssie) alebo sucinu maxtermov (napr. vyssie uvedena F2). Ak pocet vstupny premennych je n, tak mozme vytvorit 2^n mintermov alebo maxtermov, kde kazdy min/maxterm nadobuda logicku hodnotu (1/0) prave pre jedine vstupne pismeno logickej funkcie [1]
UNDF oznacuje uplne normalovu disjunktivnu formu a jedna sa o logicky vyraz tvoreny suctom mintermov. Mozme pouzit vsetky mintermy, alebo pouzijeme len tie, pre ktore logicka funkcia nadobuda hodnoty log. 1. [1]
UNKF oznacuje uplne normalovu konjuktivnu formu. Tu sa teda na rozdiel od UNDF jedna o log. Fciu tvorenu sucinom maxtermov, ale len tych ktore nenadobudaju hodnotu log. 1. [1].
Doporucujem mrknut na priklad nizsie, kde tvorime a mintermy a maxtermy z vyctu stavovych indexov a uplne idealne bude, ak si nieco z tychto prikladov spocitate ;).
Oba tieto zapisy su ekvivalentne. Ja radsej pouzivam UNDF (pretoze si nikdy neviem zvyknut ze tam, kde je 1 mam pri UNKF pouzit negaciu .. ) a preto budem pouzivat prave tuto formu zapisu, pokial nie je nutne inak.
Popis logickych funkcii
Pravdivostne tabulky
Pomocou pravdivostnej tabulky je mozne vyjadrit kazdu logicku funkciu.
Stavovy index s cba f(c,b,a) minterm Ps maxterm Ss
0 000 0 c'b'a' c + b + a
1 001 1 c'b'a c + b + a'
2 010 1 c'ba' c + b' + a
3 011 0 c'ba c + b' + a'
4 100 1 cb'a' c' + b + a
5 101 0 cb'a c' + b + a'
6 110 1 cba' c' + b' + a
7 111 0 cba c' + b' + a'
Doporucujem si pozriet aj pravdivostnu tabulku v nizsie uvedenom priklade scitacky.
Mapy
Mapy su jednou z moznosti, ako vyjadrit logicku funkciu. Mapa je plosny utvar, ktory je rozdeleny do 2^n poli, kde n je pocet nezavislych premennych logickej fcie [1]. Jedna sa teda o dvojrozmerne pole m . n, kde m aj n je mocnina 2. Podla vzajomneho priradenia policka k stavovym indexom rozdelujeme mapy na Karnaughovu mapu a Svobodovu mapu (postacuju pre nase potreby).Su vhodnym prostriedkom pre vyjadrenie log. fcii a pre minimalizaciu fcii 2 - 6 premennych.
Svobodova Mapa
Svobodova mapa najviac zodpoveda pravdivostnej tabulke. Stavove indexy su zoradene do policok, ktore nasleduju vedla seba. Ak niekde budete pocut nazov Veitchova alebo Marquandova, tak autor mal na mysli prave tuto mapu.
Karnaughova mapa
V buducnosti sa budeme zaoberat minimalizaciou logickej funkcie a pre tieto potreby sa nam viac hodi prave Karnaughova mapa. Do policok sa vzdy zapisu susedne stavy, teda kombinacie hodnot nezavislych premennych zobrazenych do policok vedla seba, sa lisia vzdy hodnotou jednej nezavislej premennej [1].
Mapu mozme zaviest aj pomocou Grayovho kodu. V takomto pripade sa pri prechode medzi susednymi stavmi bude vzdy menit len jedna premenna. Grayov kod a Karnaughova mapa s jeho vyuzitim su znazornene na obrazky nizsie.
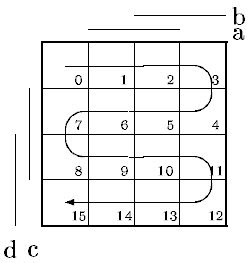
Priklad: f(d,c,b,a) = SUM(1,2,4,6,9,11,15). Znamena to, ze jednotky zapiseme do policok so stavovym indexom, ako na pravej casti fcie.
Pri viacerych nezavislych premennych zvacsujeme pocet riadkov, ziskame nove riadky posunutim u Svobodovej mapy a otocenim u Karnaughovej mapy.
Toto vyjadrenie nie je velmi nazorne a nebudeme ho pouzivat, ale slubujem, ze sa k nemu vratim a doplnim hned, ako sa dostanem k nejakemu plnohodnotnemu vyjadreniu :).
Dalsie moznosti su formy popisu logickym vyrazom a zoznamom indexov vstupnych pismen.
Formy popisu by sme mali, na tomto mieste by vsak bolo vhodne uviest si nejaky priklad, aby bolo uplne jasne o co tu vlastne ide. Uz sme uviedli, ze mapy budeme s vyhodou pouzivat pri minimalizacii logickych funkcii. Nikde sme vsak neuviedli, ako sa vlastne k takej mape dostaneme.
Priklad
Ako priklad si vyberieme scitacku. Vytvorime mapu, vyjadrime log. fcie a v dalsej kapitole si ukazeme, ako ich zminimalizujeme.
Scitacka si v tejto chvili predstavime ako black box. Na scitanie potrebujem dvoch scitancov. Vystupom je vysledok scitania. Urcite Vas napadlo, ze sa s tymto riesenim dostaneme do problemov, ak cisla budu dost velke na to, ze budeme potrebovat dalsi vstup, ktory bude sluzit ako prenos.
Teda, vstupom budu 3 premenne, a, b a p. Vystupom bude q a s, kde q bude vstupom pre dalsi prenos a s je vysledkom.
st. index a b p q s
0 1 1 1 | 1 1
1 1 1 0 | 1 0
2 1 0 1 | 1 0
3 1 0 0 | 0 1
4 0 1 1 | 1 0
5 0 1 0 | 0 1
6 0 0 1 | 0 1
7 0 0 0 | 0 0
Z pravdivostnej tabulky dostaneme nasledujuce logicke funkcie:
S = abp + ab’p‘ + a’bp‘ + a’b‘p
Q = abp + abp‘ + ab’p + a’bp
Vsimnite si, ze zapis je tvoreny suctom mintermov. Jedna sa teda o UNDF.
Ak by sme chceli pouzit UNKF, tak by nas vysledok vyzeral takto:
S = (a+b+p) . (ab’p‘) . (a‘ + b + p) . (a’ + b + p‘) . (a’ + b‘ + p)
Q = (a’+b’+p) . (a’+b+p‘) . (a+b’+p‘) . (a+b+p)
Priklad
f(c,b,a) = SUM(0,1,5,6,7) (teda vycet stavovych indexov, kde f nadobuda log. hodnoty 1)
Aby sme si to vedeli predstavit, tak si vypiseme pravdivostnu tabulku. Vsimnite si, ako priradujeme hodnoty jednotlivym premennym, ak sa na chvilku zamyslite, tak Vam to isto da logiku J.
s c b a f(c,b,a)
0 0 0 0 1
1 0 0 1 1
2 0 1 0 0
3 0 1 1 0
4 1 0 0 0
5 1 0 1 1
6 1 1 0 1
7 1 1 1 1
UNDF: z vyssie uvedenj definice vyplyva, ze pouzijeme vsetky mintermy, alebo len tie, kde f(c,b,a) nadobuda log. 1. A kedze clovek je tvor lenivy a my nie sme vynimky, tak vypiseme len tie mintermi, kde fcie nadobudne 1.
· Z tabulky vyberieme len riadky, kde f(c,b,a) = 1
· Jedna sa mintermy, takze budeme tvorit sucin
· Kazdu premennu, ktora je rovna 0 znegujeme
· Kedze sa jedna o UNDF, tak medzi mintermami bude sucet
UNKF: opat hodime okom na vyssie uvedenu fciu a zistime, ze pouzijeme maxtermy, ale len tie, ktore nenadobudaju hodnotu log. 1. Pouzijeme teda sposob, ako pri UNDF s „mensimi“ odchylkami.
· Z tabulky vyberieme len riadky, kde f(c,b,a) = 0
· Jedna sa maxtermy, takze budeme tvorit sucet
· Kazdu premennu, ktora je rovna 1 znegujeme
· Kedze sa jedna o UNKF, tak medzi maxtermami bude sucin
(c+b’+a) . (c+b’+a‘) . (c’+b+a)
Karnaughova mapa
Takto vyzera Karnaughova mapa, v ktorej su zapisane stavove indexy. Vsimnite si, ako koresponduje s pravidvostnou tabulkou. Napriklad pre s = 0 su hodnoty premennych a,b,c = 0 ako v tabulke, tak v mape.
A takto vyzera ked je vyplnena. Ak porovnate mapu vyssie (tu s tymi farebnymi ciarami J ) a nasledujucu mapu a pravdivostnu tabulku, tak urcite zistite, ze lahsie to uz snad byt nemoze J.
---------- b
----------- a1 1 0 0
c| 0 1 1 1Svobodova mapa
Tiez nic zloziteho, ale davajte si pozor na rozlisne priradenie stavovych indexov k jednotlivym polickam mapy. Ak to spachate zle, tak vam to nebude sediet.
------------- b
--- --- a
0 1 2 3
c| 4 5 6 7tabulku vyplnime:
------------ b
--- --- a
1 1 0 0
c| 0 1 1 1Priklad
f(c,b,a) = PI(1,2,5,6) (teda vycet stavovych indexov, kde f nadobuda log. hodnoty 0)
s c b a f(c,b,a)
0 0 0 0 1
1 0 0 1 0
2 0 1 0 0
3 0 1 1 1
4 1 0 0 1
5 1 0 1 0
6 1 1 0 0
7 1 1 1 1
Karnaughova mapa:
------------- b
------------ a
1 0 1 0
c | 1 0 0 1
Svobodova mapa:
--------------b
--- --- a
1 0 0 0
c | 1 1 0 1
UNKF: (a' + b + c) . (a + b' + c) . (a' + b + c') . (a + b' + c')
UNDF: a'b'c' + abc' + a'b'c + abc
Good luck ;)
Pouzita literatura:
[1] Logicke obvody, Kubatova, FEL CVUT Praha








